UNIT 4 CIRCULAR FUNCTIONS - Degree and Radian Measure 1

Hi Everyone, It's Jade! 

Yesterday, we started our new unit about Circular Functions and we just got the thickest booklet so far. Yey! More pages, More fun! 



Before we proceeded to our first topic, we first reviewed a little bit about pi.

We defined pi as the measurement of the angle of a circle.

Its is equal to 3.141592653589793238462643383279502884197169399375105

8209749445923078164062862089986280348253421170679......, but we don't need to memorize that, just remember that it is equal to 3.14 and you are good to go.

So here's the first topic:

DEGREE and RADIAN MEASURE 

An angle is determined by two rays.

We define an angle of rotation by rotating a ray about its endpoint, creating a vertex.

The starting point of the ray is called the initial side, and the position after rotation is called the terminal side.

Angles can be measured using different units, such as revolutions, rotations, degrees, radians, and gradians.

Angle measure without units are considered to be radians

          Ex. 2.5 radians

Angle measure in degrees must show the degree symbol

          Ex. 90°, 30°

Obtuse angles measure greater than 90°.

Acute angles measure less than 90°

 If the rotation of the ray is in a counter-clockwise direction, we consider the angle to be positive.

 If the rotation of the ray is in a clockwise direction, we consider the angle to be negative.

An angle in a coordinate plane is said to be in standard position if:

     a. its vertex is at origin

     b. its initial side is on the positive x-axis

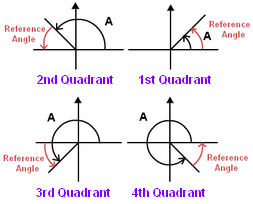
A reference angle is the measure of the angle between terminal arm and the x-axis.

RADIAN MEASURE is another way to measure angle in a circle.

When the arc of a circle has the same length as the radius of the circle, the measure of the central angle that intercepts the arc is 1 radian.

• angle is equal to 1 radian when radius is equal to arc length (when r = a)
• when radius is not equal to arc length, the angle will be greater than or less than 1 radian
• to convert to radian multiply the degree measure by pi/180°

• 
  
• to convert to degrees multiply the radian measure by 180°/pi

• pi = 3.1416.... in radian measure but pi = 180° in degree measure.

We can use this information to translate revolutions into radian measure...

THAT'S PRETTY MUCH IT!!!!

REMINDER:

Polynomial Functions Assignment 2 is due tomorrow, Friday, March 21st 2014

Transformation Golf Project is due on Monday, March 24th 2015

Polynomial Functions Test is on Tuesday, March 25th 2014