No explanation needed.

Unit 4 - Circular Functions - The Unit Circle I

Hi, I'm Navdeep!

I'm going to scribe about the second topic in Unit - 4 "Circular Functions" and the topic is called The Unit Circle I.

A unit circle is the circle with its centre at the origin and with a radius of one unit. Equation of the unit circle is x² + y² = 1.

Its standard position starts at (1,0).

Positive distance is measured in a counterclockwise direction; and negative distance is measured in a clockwise direction. 

Terminal Point is where the terminal arm of an angle ϴ intercepts the unit circle. For every arc. length ϴ on the unit circle, P(ϴ) is unique. 

 

Always remember, if r = 1, then:

sinϴ                      =            O/H            =              y/r                = y/1 = y

cosϴ                     =            A/H            =              x/r                = x/1 = x

tanϴ                      =            O/A            =              y/x               = sinϴ/cosϴ

So, that's why P(x,y) = P(cosϴ, sinϴ), and since x² + y² = 1, we have cos²ϴ + sin²ϴ = 1.

But if the circle has a centre with its origin and radius is other than one 1, the equation would be 

x² + y² = r².

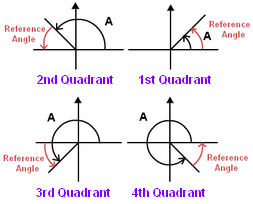
CAST Rule

For example: Given that sinϴ = -⅘ and cosϴ = ⅗, in which quadrant does ϴ lie?

 We know that sin is negative and cos is positive given in the question. So now according to the CAST Rule ,we know that we have sin negative and cos positive in Quadrant IV. 

If we have to determine the coordinates of on the unit circle when we have one of the coordinate is given and have to find the other so we can use
x² + y² = 1.

For example: the y-coordinate is -⅟₂ and the point is in Quadrant III and determine the x-coordinate.

We can use this equation to solve for x by substituting the value of y:
x² + y² = 1x² + (-⅟₂)² = 1x² + ⅟₄ =1x² = 1 - ⅟₄x² = 3/4x = ±√3/4

Special Right Triangles

Now we have to understand and memorize the reciprocal trigonometric functions too with their new names as follows:  

Just don't try only to memorize them but try to understand that how all of them are related to each other!

Reference Triangles

There are two reference triangles: one with the angles of 45+45+90 degrees and the other one with 30+60+90 degrees. 

Let's look at the example of a reference triangle with the angles of 45+45+90 degrees:

Quadrantal Angles

There are three different quadrantal angles and can be written in degrees, in exact values and in approximate values. Take a look at the following example:

So in this example, first circle shows the angles in degrees, second shows in radians as exact values, and the third one shows in decimals as approximate values.

UNIT CIRCLE

       So, this is the unit circle and we have a similar diagram as above in the booklet too and if anyone has not finished filling in this unit circle due to any kind of confusion or then hope it is helpful. 

      Hope all above would be helpful and have a great day!!

The End!

UNIT 4 CIRCULAR FUNCTIONS - Degree and Radian Measure 1

Hi Everyone, It's Jade! 

Yesterday, we started our new unit about Circular Functions and we just got the thickest booklet so far. Yey! More pages, More fun! 



Before we proceeded to our first topic, we first reviewed a little bit about pi.

We defined pi as the measurement of the angle of a circle.

Its is equal to 3.141592653589793238462643383279502884197169399375105

8209749445923078164062862089986280348253421170679......, but we don't need to memorize that, just remember that it is equal to 3.14 and you are good to go.

So here's the first topic:

DEGREE and RADIAN MEASURE 

An angle is determined by two rays.

We define an angle of rotation by rotating a ray about its endpoint, creating a vertex.

The starting point of the ray is called the initial side, and the position after rotation is called the terminal side.

Angles can be measured using different units, such as revolutions, rotations, degrees, radians, and gradians.

Angle measure without units are considered to be radians

          Ex. 2.5 radians

Angle measure in degrees must show the degree symbol

          Ex. 90°, 30°

Obtuse angles measure greater than 90°.

Acute angles measure less than 90°

 If the rotation of the ray is in a counter-clockwise direction, we consider the angle to be positive.

 If the rotation of the ray is in a clockwise direction, we consider the angle to be negative.

An angle in a coordinate plane is said to be in standard position if:

     a. its vertex is at origin

     b. its initial side is on the positive x-axis

A reference angle is the measure of the angle between terminal arm and the x-axis.

RADIAN MEASURE is another way to measure angle in a circle.

When the arc of a circle has the same length as the radius of the circle, the measure of the central angle that intercepts the arc is 1 radian.

• angle is equal to 1 radian when radius is equal to arc length (when r = a)
• when radius is not equal to arc length, the angle will be greater than or less than 1 radian
• to convert to radian multiply the degree measure by pi/180°

• 
  
• to convert to degrees multiply the radian measure by 180°/pi

• pi = 3.1416.... in radian measure but pi = 180° in degree measure.

We can use this information to translate revolutions into radian measure...

THAT'S PRETTY MUCH IT!!!!

REMINDER:

Polynomial Functions Assignment 2 is due tomorrow, Friday, March 21st 2014

Transformation Golf Project is due on Monday, March 24th 2015

Polynomial Functions Test is on Tuesday, March 25th 2014

Analyzing Graphs of Polynomial Functions

Hi! I'm Marielle! (I'm using Mydee's account just because)

Last Monday, March 17, we were assigned to determine the following for Example 1 a and b:

• The least possible degree
• The sign of the leading coefficient
• The x-intercepts and the factors of the function with least possible degree
• The intervals where the function is positive and the intervals where it is negative

*NOTE: This topic is more like a wrap up of the previous lessons from this unit involving graphs

The graphs are:

a.)

 

• Basically, to find the least possible degree of this graph, determine how many x-intercepts there are. In this case, the points are -4, -2, and 2, so the degree of this polynomial function is three.
  
  

• Next, we have to figure the sign of the leading coefficient! For this graph, the sign of the leading coefficient is positive because the function runs down quadrant 3 rises up quadrant 1.
  
  

Moving on~

• Now we have to get the factors of the function. This one should be simple since all you have to do is go back to the zeroes (which are -4, -2, 2) and change them into factors by getting their absolute values [(x+4), (x+2), (x-2)]
  
  

• Lastly, the intervals where the function is positive and the intervals where it is negative.

Positive:

x > 2

-4 < x < -2

Negative:

x < -4

-2 < x < 2

b.)

This function is almost  the same as the first one above, however, this one has different set of values.

The Degree is 3 and sign of the leading coefficient is still positive.

The x-intercepts of this function are -5, -1, 4; while the factors are (x+5) (x+1) (x-4)

The positive intervals will be:

x>4

-5<x<-1

and the negative intervals:

x<-5

-1<x<4

For a different mind exercise, we sketched the given polynomial functions to the graph! And one of the easy ones is the function:

y = (x-1)(x+2)(x+3)

Degree	3
Leading Coefficient	+ve
End Behaviour	Goes down to the 3rd quadrant, rises up at 1st quadrant
Zero/x-intercepts	1, -2, -3
y - intercept	-6
Intervals when the function is +ve or -ve	+ve:                              -ve:                 x>1                               x<-3        -3<x<-2                        -2<x<1

This table will be sketched/plotted as:

Again, the degree is 3 because there are three zeroes plotted and the Leading coefficient is positive.

The End Behaviour of the function is it slumps down the third quadrant and rises up the 1st quadrant

The x-intercepts are 1, -2, -3 as presented above

Y-intercept is -6 because we have transform all of the x in every factor [(x-1)(x+2)(x+3)] to zero and solve.

*NOTE: If you want to know how high the function will “bounce” in between points -3 and -2, your best bet is to transform all x’s in the factors again with every value in between the said points.

So, that will be it! I hope this will help you for review purposes and sorry if it won’t and confused you instead.

Either way, hope you will all have a good day ~

 

Matching and Graphing Polynomial Functions

Hello, I'm Alesandro.

This March 12th we learned about matching polynomial functions to their graphs and graphing polynomial functions.

First, you must identify various parts and characteristics of a polynomial function to be able to picture and graph it.
These characteristics include:

• Type of function, degree, and end behaviour


• A function with an even degree would start and end in the same direction  
• (x → -∞ ; f(x)→ + ∞ ) (x → + ∞ ; f(x)→ + ∞ )
• A function with an odd degree would rise and fall
• (x → -∞ ; f(x)→ - ∞ ) (x → + ∞ ; f(x)→ + ∞ )

• Possible x-intercepts ( y = 0 )
• Number of x-intercepts vary depending on degree
• Possible y-intercept ( x = 0 )
• Maximum or Minimum value

If you are tasked with matching graphs, the easiest method would be to determine the y-intercept. This is when x is given the value of 0 and the y-intercept would be the last term, or the term without the variable of x.

Now let's get to graphing.

• To be able to graph a polynomial function, use the x-intercepts, the y-intercept, the degree of the function, and the sign of the leading coefficient.
• x-intercepts are the roots of the corresponding polynomial equation (x-intercepts of a quintic function would be the roots of the quartic equation, and so on)
• The zeroes are factors of the polynomial function
• The factor theorem is used to express the factored form of a polynomial function

Steps:

1. Factor the equation
2. The sign of the leading coefficient should be stated and the end-behaviour arrows drawn.
• The sign of the leading coefficient determines the direction the end-behaviour arrows go to.
• The degree determines the placement of the end-behaviour arrows as well.
• An odd degree with a positive leading coefficient would have the left arrow go down (QIII) and the right would go up (QI)
• An odd degree with a negative leading coefficient would have the left arrow in QII and the right at QIV
• An even degree with a positive leading coefficient would have the arms both go up (QI and QII);
• An even degree with a negative leading coefficient will have both arrows go down (QIII and QIV)
3. Plot the zeros, the y-intercept, and connect them by using curved lines

Note: 

To determine the lowest or highest point (where the curve line will turn) between two points, you must substitute x for a value between the two given points.
   If the curve is between (2,0) and (4,0) the curve would be located between these two points such as (3,y)

Important Graphing Rules:

1. If the root of the equation is unique (not having two or more of the same root) the curve passes the x-axis at that point.

     2. If there are two or more of the same root:

• An even number of the same root would cause the curve to bounce off at the x-axis

             

• An odd number of the same root would cause the curve to cross at that point in the x-axis

    3. The higher the degree, the more the graph flattens out at this point.

That's all guys and thanks for your time!

Note²:  Lack of unit booklet images brought to you by a non-responding camera on a smartphone and a       malfunctioning scanner. Sorry.

Note³: If you have trouble imagining graphs and afraid of downloading software, a free graphing calculator is available online @ https://www.desmos.com/calculator

Integral Zero Theorem

Integral Zero Theorem

Hey guys this is Jose and today I will be spamming this blog with pictures and examples!

When factoring a polynomial p(x), it is helpful to know which integer values of a to try when determining if p(a) = 0. Consider the polynomial p(x) = x^3 - 7a^2 +14x - 8. If x =a satisfies p(a)  = 0, then a^3 - 7a^2 +14a- 8 =0 or a^3  -7a ^ 2+ 14a - 8 = 0. or a^3 - 7a^2 + 14a = 8. Factoring out the common factor on the left side  of the equation gives the product a(a^2 - 7a +14) = 8. Then, the possible integer  values for the factors in the product on the left side are factors of 8. +/-1,+/-2,+/-4 and +-8.


The relationship between the factors of a polynomial and the constant term of the polynomial is stated in the Integral Zero Theorem.

*NOTE*

Integral Zero Theorem States that if x - a is a factor of a polynomial function p(x) with integral coefficients, then a is a factor of the constant term of p(x)

Example: (1)

                  (2)      

                    (3)           

And here is a picture  for those who couldn't comprehend this .

                                                   Mr. Piateck          

Student 

We also did some  High-Degree Polynomials tuturu!!!!

*VERY IMPORTANT (PROVINCIAL EXAM) TYPE OF QUESTION*

*An Intermodal container that has the shape of a rectangular prism has a volume, in cubic feet, represented by the polynomial function  V(x) = x^3 + 7x^2 - 28x +20, where x is a positive real number, What are factors that represent possible dimensions, terms of x, of the container?*

This Is The End of The Blog now take a break and go eat.